La compréhension de la dynamique d’une épidémie, notamment dans la situation actuelle marquée par la propagation du COVID-19, est fondamentale afin de pouvoir en appréhender de manière adéquate les risques associés. Différents modèles relativement intuitifs permettent d’expliquer une dynamique de contamination par le COVID-19 . Toutefois ces derniers ne peuvent être utilisés à des fins de prédiction car ils reposent sur de multiples approximations et ne permettent pas par là-même, de reproduire la dynamique pandémique associée à diverses catégories d’individus. Pour pallier ces difficultés, les épidémiologistes ont le plus souvent recours à des modèles de type SIRD qui permettent de dynamiser en temps réel quatre compartiments (Susceptibles – Infectés – Rétablis – Décédés) de la population ainsi que leurs interactions respectives.
Le présent billet a pour objectif de détailler une modélisation SIRD et de l’appliquer à des séries de données françaises associées à la propagation du COVID-19.
Les compartiments d’une modélisation SIRD
Une modélisation de type SIRD repose sur une segmentation, à chaque date, de la population sous-jacente selon plusieurs compartiments : les individus non contaminés Susceptibles de contracter la maladie (compartiment S), les personnes Infectées (compartiment I), les individus Rétablis préalablement infectés (compartiment R) et enfin les personnes Décédées suite à leur infection par le virus (compartiment D).
Le plus souvent en première approximation dans une modélisation SIRD, un individu rétabli est considéré comme immunisé contre la maladie[2].
Dans certaines versions avancées de modèles SIRD, la période d’incubation est prise en compte pour la projection des différents compartiments. À des fins didactiques, le modèle détaillé par la suite n’intégrera pas cette spécificité.
Le diagramme suivant permet d’illustrer les transitions possibles entre chacun des états considérés:
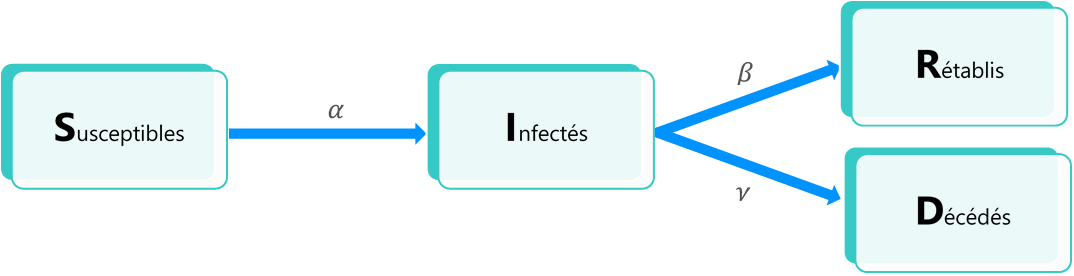
Où le paramètre α (resp. β, γ) correspond au taux d’infection (resp. de rétablissement, de létalité) du modèle. Ces éléments sont détaillés infra.
En notant S(t), I(t), R(t) et D(t) respectivement le nombre cumulé de cas susceptibles, infectés, rétablis et décédés en (le plus souvent pour une unité de temps journalière), l’évolution du nombre d’individus dans chaque compartiment peut être approximée par le système d’équations suivant :
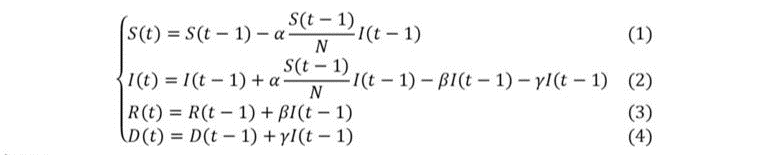
- la taille initiale de la population considérée ;
- le taux d’infection : cette quantité est homogène au produit d’une probabilité de contamination avec un nombre moyen d’individus rencontrés par une personne infectée à chaque unité de temps. Ce paramètre est ajusté de la fraction de population contaminable (quantifiée par le ratio ), afin de tenir compte de l’épuisement du nombre de susceptibles avec le temps ;
- le taux de rétablissement: il s’agit du taux moyen d’individus infectés qui se rétablissent par unité de temps. Son inverse représente la durée moyenne de rétablissement d’un patient infecté ;
- le taux de létalité : il s’agit du taux moyen d’individus infectés qui décèdent par unité de temps.
Le nombre de reproduction de base : définition et estimation
Un des principaux indicateurs de suivi de la contagiosité d’une épidémie est son nombre de reproduction, noté ℜ0. Il s’agit du nombre moyen de personnes contaminées par un individu infecté, durant sa période de contagiosité.
Lorsque ℜ0 est supérieur (resp. inférieur) à 1, l’épidémie se propage (resp. s’éteint progressivement).
Dans une modélisation SIRD, le nombre de reproduction se calcule de la manière suivante :
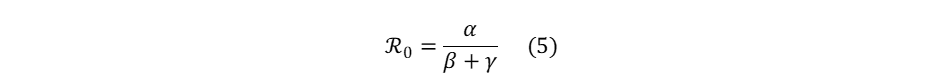
Différentes approches empiriques permettent d’estimer la valeur de ℜ0 sur des séries de données épidémiologiques.
Sous des hypothèses d’équivalence S ≈ N (i.e. le nombre de susceptibles reste proche de la taille de population initiale), on observe que :
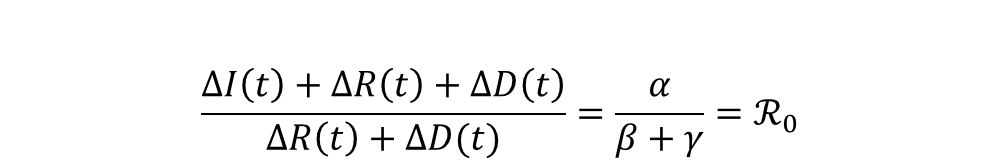
Il en découle donc une approche d’évaluation du nombre de reproduction par régression linéaire de la série (CΔI(t) + CΔR(t) + CΔD(t))t sur la série (CΔR(t) + CΔD(t))t.
Où CΔI(t), CΔR(t) and CΔD(t) représentent les incréments cumulés[3] respectifs de I, R et D entre l’instant initial et t.
Le paramètre ℜ0 correspond alors à la pente associée à la régression linéaire détaillée ci-dessus. Cette méthode d’évaluation est notamment présentée dans l’article de CLEO et al. [3].
Par ailleurs, comme évoqué supra, ℜ0 est un indicateur fondamental permettant de rendre compte de la contagiosité d’un épisode pandémique, puisqu’il permet d’en caractériser le potentiel de dissémination. Si la condition α > β + γ est vérifiée alors l’épidémie est amenée à se propager. Dans le cas contraire (i.e. if α < β + γ) , alors l’épidémie s’éteint progressivement.
Méthodes d’estimation des paramètres du modèle SIRD
Différentes approches permettent une estimation empirique des taux de rétablissement et de létalité sur les séries de données associées au COVID-19. La méthode considérée dans ce document, basée sur une régression linéaire, est conforme à la technique détaillée par CLEO et al. [3].
Une analyse approfondie du modèle SIRD conduit à des estimations des taux de rétablissement de létalité par régression linéaire des séries (ΔR(t))t et (ΔD(t))t sur la série (CΔI(t – 1) – CΔD(t – 1) – CΔR(t – 1))t.
Les estimateurs des paramètres β et γ correspondent ainsi aux pentes des régressions linéaires détaillées ci-dessus.
Enfin, il est possible de dériver la valeur du paramètre de taux d’infection α à partir de l’équation caractérisant le nombre de reproduction et des estimations des précédents facteurs. Ce taux est par conséquent estimé comme suit :
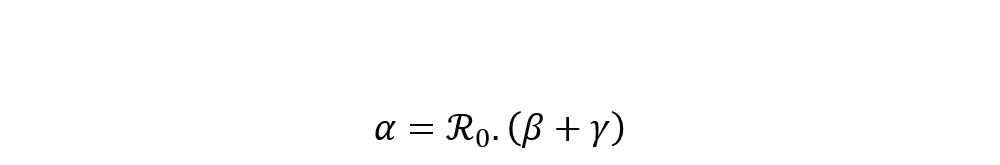
Une approche alternative pour estimer les taux d’infection, de rétablissement et de létalité, consiste à minimiser la somme des écarts quadratiques entre les valeurs observées et théoriques des nombres d’infectés, de décès et de rétablis. En pratique, cela revient à résoudre le programme d’optimisation suivant :
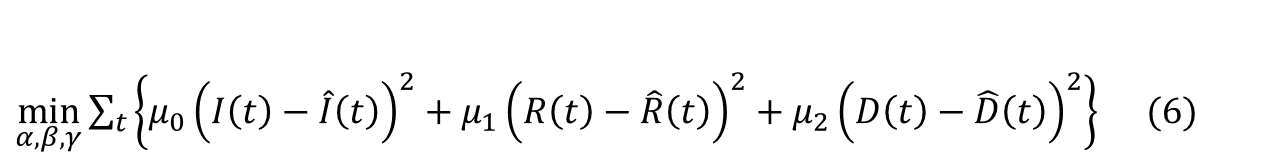

Calibrage du modèle SIRD sur les données françaises COVID-19
Les paramètres du modèle épidémiologique SIRD ont été calibrés sur les données françaises, pour la période comprise entre le 21/02/2020 et le 20/04/2020[4].
Le nombre de reproduction de base obtenu par régression linéaire sur les données comprises dans la première phase épidémique s’élève à 2,93. Cette grandeur est conforme aux évaluations publiées par différents experts depuis le début de la crise du COVID-19. Le lecteur intéressé pourra notamment consulter Massonnaud et al. [5] ainsi que le rapport de l’Imperial College COVID-19 Response Team [6].
La figure 1 illustre l’évolution du taux de rétablissement estimé par régression linéaire basée sur les séries précédemment introduites. Afin de garantir la robustesse d’estimation de ce paramètre et d’éliminer certaines valeurs aberrantes observées, l’estimation de ce paramètre a été réalisée sur une plage d’historique plus récente.
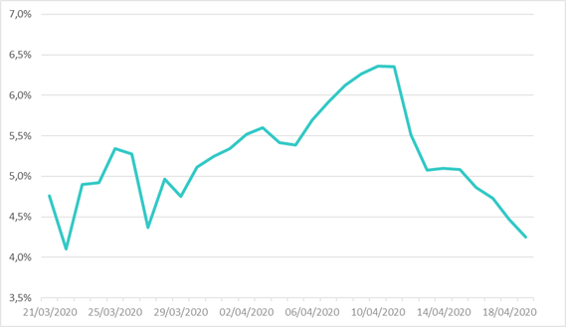
Figure 1 : Taux de rétablissement du modèle SIRD estimé sur données françaises entre le 21 mars et le 19 avril
Le graphique fait apparaître un changement de tendance dans le profil des valeurs de ce paramètre ; la date pivot correspondant peu ou prou au pic de l’épidémie. Le taux estimé s’élève en moyenne à 5,23% ce qui correspond à une durée de rétablissement d’environ 19 jours.
Le taux de létalité est également estimé par une approche de type régression linéaire basée sur les séries introduites supra. Pour les mêmes raisons que celles évoquées pour la représentation du taux de rétablissement, l’estimation de ce paramètre a été réalisée sur une plage d’historique plus récente.
Le graphique ci-après illustre le profil de ce paramètre :
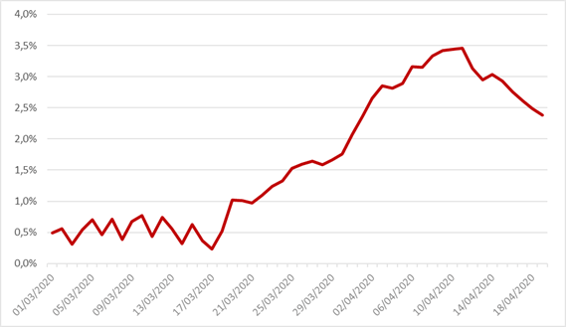
Figure 2: Taux de létalité du modèle SIRD sur données françaises entre le 1er mars et le 19 avril
La valeur moyenne de ce paramètre sur la plage étudiée s’élève à 1,67%.
L’ordre de grandeur de ce paramètre est conforme aux estimations qui figurent dans la littérature académique. Le lecteur intéressé pourra par exemple consulter le document [4] (Society of Actuaries Research Brief Impact of COVID-19), qui fournit notamment une synthèse des valeurs du taux de létalité associé au COVID-19 dans plusieurs zones géographiques et à différents stades de développement de l’épidémie.
Le taux d’infection est dérivé des estimations du nombre de reproduction ℜ0 et des paramètres β et γ, sa valeur moyenne est de 20,22%.
Cette estimation est cohérente avec le niveau moyen de croissance journalière observée sur les séries de cas confirmés :
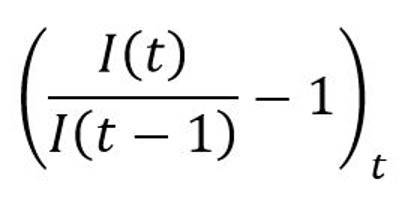
qui sous hypothèse d’une diffusion SIRD et sous condition d’équivalence S ≈ N, doit être proche de la quantité α – β – γ. . La valeur du taux de croissance des confirmés sur la période comprise entre le 1er mars et le 20 avril 2020 s’élève à 16,52%, ce qui conduit à un taux d’infection de 23,42% homogène à l’estimation de 20,22% obtenue ci-dessus.
A l’issue de la phase de calibrage, les nombres cumulés observés et théoriques induits par le modèle SIRD ont été comparés au 20 avril 2020, le tableau suivant en restitue les valeurs :
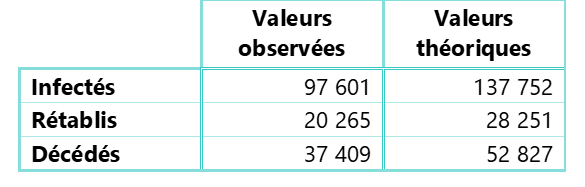
Tableau 1 : Cas cumulés observés et théoriques des compartiments I, R et D sur données françaises au 20/04/2020
Les effectifs théoriques obtenus sont supérieurs aux nombres observés. Cette surestimation s’explique notamment par l’entrée en vigueur en France, de mesures de confinement le 17 mars 2020. Ce dispositif a conduit à atténuer significativement la dynamique du COVID-19 alors même que certains paramètres estimés sur la première phase du développement de l’épidémie peuvent conduire à une sévérisassions du risque projeté.
Conclusion
Le modèle SIRD présenté dans le cadre de ce billet, constitue une première approche de modélisation pandémique reposant sur différents compartiments de la population ainsi que leurs interactions respectives.
Toutefois afin d’améliorer la capacité prédictive du modèle, il apparaît nécessaire d’apporter plusieurs évolutions à l’approche mise en œuvre.
À titre d’exemple, il est possible de citer les problématiques de retraitement des nombres d’infectés et de rétablis devant être corrigés afin d’intégrer les cas asymptomatiques qui, dans le cas du COVID-19, atteignent des proportions très élevées (la recherche médicale fait mention d’ordres de grandeur d’environ 50% à 60% de cas asymptomatiques).
A cette correction des données, doit être associée une évolution du modèle SIRD permettant d’intégrer un compartiment dédié à la projection des individus asymptomatiques. Ceci majore sensiblement le nombre de paramètres SIRD à estimer, mais conduit toutefois à une meilleure réplication de la dynamique pandémique.
Ces techniques de traitement des données et de modélisation seront présentées dans un prochain billet.
Laurent DEVINEAU, Executive Partner
Carolina RAMIREZ, Regional Head of Consulting
Kevin POULARD, Actuarial R&D Leader
Auriol WABO, Consultant
[1] Les ressorts d’une dynamique épidémiologique – https://www.actuaris.fr/actualite/les-ressorts-dune-dynamique-epidemiologique/
[2] Source data.gouv.fr – https://www.data.gouv.fr/fr/datasets/coronavirus-covid19-evolution-par-pays-et-dans-le-monde-maj-quotidienne/
[3] Cleo et al., Data-Based Analysis, Modelling and Forecasting of the COVID-19 outbreak, mars 2020
[4] Society of Actuaries Research Brief Impact of COVID-19 – April 16, 2020
[5] Massonnaud et al., COVID-19: Forecasting short term hospital needs in France, mars 2020
[6] Imperial College COVID-19 Response Team, Impact of non-pharmaceutical interventions to reduce COVID-19 mortality and healthcare demand, mars 2020

