Comprendre la dynamique d’une épidémie : Modèles mathématiques et application au COVID-19
Le suivi régulier des nombres de cas confirmés d’infections par le COVID-19 fait apparaître des profils, par pays ou à l’échelle mondiale, à croissance particulièrement accélérée. Cette cinétique est caractéristique de toute dynamique épidémiologique et repose sur le fait que chaque cas de contamination se démultiplie au gré des brassages des populations sous-jacentes, en plusieurs cas d’infections par unité de temps.
L’objectif de ce billet est d’expliciter de manière didactique les ressorts d’une dynamique épidémiologique.
D’une propagation épidémiologique exponentielle…
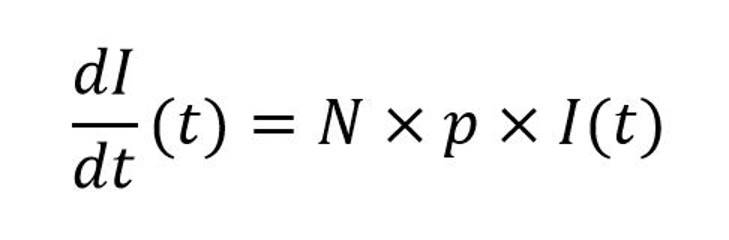
Avec N le nombre moyen d’individus qu’une personne infectée rencontre à chaque unité de temps et la probabilité qu’une personne exposée soit infectée.
En notant a = N . p, fréquemment dénommé « taux d’infection », la résolution de cette équation conduit à un profil exponentiel du nombre de cas confirmés, similaire à ce qui peut être observé lors de la phase de développement actif de la pandémie :
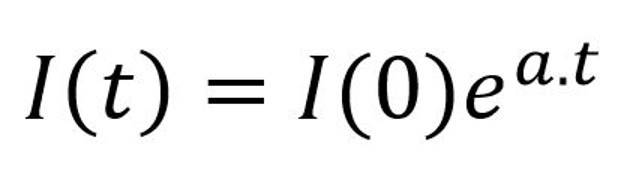
Parmi les indicateurs de suivi de l’épidémie, la période de doublement constitue une mesure particulièrement clé. Elle correspond au nombre de jours conduisant à un doublement de la population d’infectés et dans le cadre d’une dynamique exponentielle, elle est évaluée comme suit :
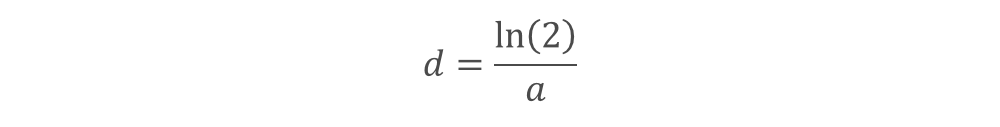
À titre illustratif, pour un taux d’infection de 30% (ordre de grandeur observé les premiers jours de développement de l’épidémie avant mise en place des politiques de confinement), la période de doublement est d’environ 2,3 jours.
… à une convergence logistique
En pratique le développement du nombre de cas confirmés ne correspond pas à une dynamique exponentielle. Cette dernière ne parvenant pas à rendre compte de l’atténuation régulière des populations de « susceptibles » (terme dédié pour désigner les individus contaminables).
En effet, le nombre moyen de personnes qu’un individu infecté rencontre à chaque unité de temps, doit être réduit de la fraction de population infectée, afin de tenir compte de l’épuisement du nombre de susceptibles avec le temps :
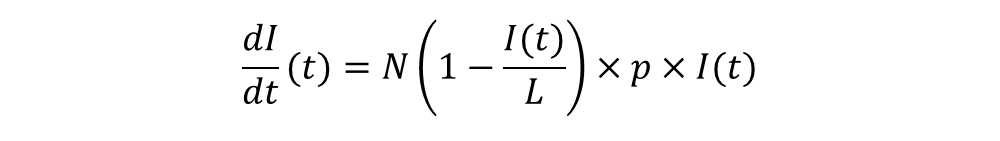
Modèle de Verhulst et dynamique logistique
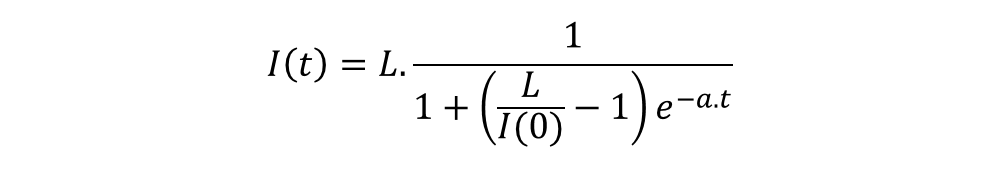
Cette fonction, dénommée le plus souvent « fonction logistique », induit des profils relativement fidèles à ceux des nombres de cas confirmés cumulés observés sur un épisode pandémique intégralement développé (e.g. cas de l’épidémie de COVID-19 en Chine).
Quelques illustrations : Ajustement du modèle de Verhulst aux données chinoises
La fonction objectif considérée correspond à la somme des écarts quadratiques entre les nombres de cas confirmés cumulés observés et théoriques.
Le graphique ci-dessous illustre l’ajustement de la dynamique de Verhulst sur les cas confirmés chinois hors Hubei.
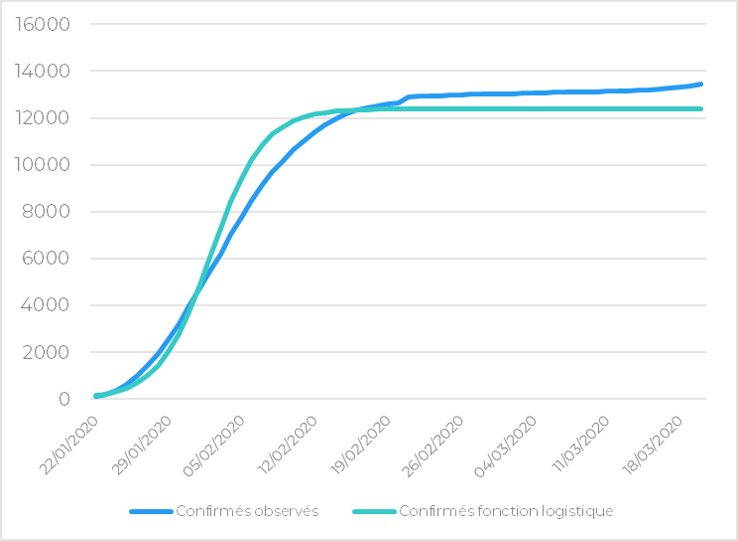
Figure 1 : Cas confirmés cumulés observés et théoriques (Chine hors Hubei)
Analyse des incréments de cas confirmés
La fonction logistique présente certaines spécificités, répliquant de manière adéquate les faits stylisés d’une dynamique épidémiologique. Sur la phase de développement actif de la pandémie, son profil est localement similaire à celui d’un développement exponentiel dont le taux d’infection s’ajusterait avec le temps.
La variation du nombre de cas confirmés par unité de temps (i.e. les quantités I (t + 1) – I (t)) est bien croissante sur la première phase pandémique puis décroît progressivement. Ce mécanisme pivot, autour d’un point d’inflexion (convexité de la fonction en début d’épidémie puis concavité à la fin), permet de caractériser le pic épidémique, particulièrement surveillé par les autorités sanitaires.
Le graphique suivant fournit une comparaison des incréments de cas confirmés observés et théoriques sur les données chinoises hors Hubei.
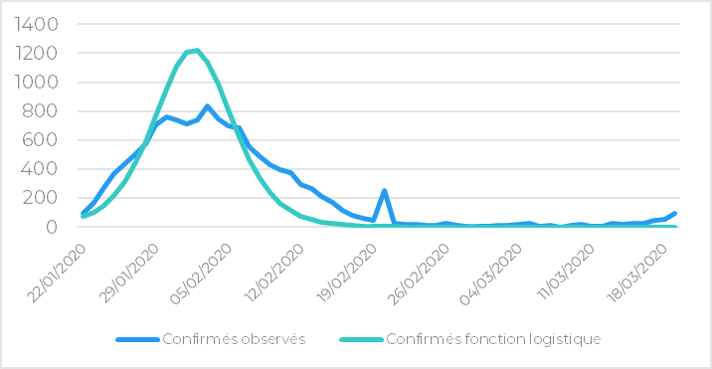
Figure 2 : Incréments journaliers des cas confirmés observés et théoriques (Chine hors Hubei)
Les graphiques ci-dessus permettent d’identifier un pic épidémique sur le cluster Chine hors Hubei autour du 04/02/2020 avec une variation maximale journalière de cas confirmés atteignant les 835 individus. prochain décryptage.
Conclusion
Les dynamiques exponentielle et logistique permettent d’expliquer en première approximation, l’accélération du processus de contamination d’un événement pandémique. Pour l’ensemble des pays touchés par la propagation du COVID-19, la croissance des cas confirmés sur la phase de développement actif de l’épidémie, est relativement conforme à un profil exponentiel.
Néanmoins, et ce indépendamment des politiques de confinement mises en œuvre en pratique, le modèle de Verhulst est plus adéquat pour restituer une dynamique pandémique car il permet d’intégrer mécaniquement le phénomène d’épuisement de la population des susceptibles dans la propagation progressive de l’épidémie.
Cependant, ces modèles simplifiés ne peuvent constituer en tant que tels, des outils prédictifs performants pour produire des anticipations réalistes du développement à moyen terme de la pandémie. Pour ce faire, il est nécessaire de considérer des modèles épidémiologiques dédiés, permettant de dynamiser en temps réel différents compartiments de la population ainsi que leurs interactions respectives. C’est notamment le cas des modèles de type SIRD (Susceptibles – Infectés – Rétablis – Décédés) qui feront l’objet d’un prochain décryptage.
Un article rédigé par les experts Addactis
Laurent Devineau, Executive Partner
Marielle de La Salle, Head of Modeling Lab
Carolina Ramirez , Regional Head of Consulting
Auriol Wabo, Consultant
[1] En raison d’une discontinuité induite par l’évolution autour du 12/02/2020 de la méthodologie de comptage des données associées à la province de Hubei, ces données n’ont pas été considérées pour cette illustration.
[1] Source Johns Hopkins University – https://github.com/CSSEGISandData/COVID-19